Zero-Knowledge-Proofs: Was sind zk-STARKs und wie funktionieren sie? (zk-Stark V2)
Was ist Proof-of-Reserves und Zero-Knowledge-Proof?
Proof-of-Reserve (PoR)
Dies ist ein Verfahren für Kryptowährungsbörsen, um zu zeigen, dass sie über genügend Vermögenswerte verfügen, um alle Kundenkonten abzudecken. Dies schafft Vertrauen, indem bewiesen wird, dass die Börse keine Verbindlichkeiten verbirgt. Der einfachste Weg, dies zu zeigen, besteht darin, sowohl die Vermögenswerte der Börse als auch eine Liste der Benutzerkonten zu veröffentlichen, damit jeder Folgendes bestätigen kann:
Die gesamten Vermögenswerte, die OKX zu halten beansprucht, sind die Summe des gesamten Vermögens jeder Benutzerin und jedes Benutzers
Das Gesamtguthaben jeder Benutzerin und jedes Benutzers beträgt mehr als null, und ihre oder seine Vermögenswerte sind erfasst, decken ihre seine Verbindlichkeiten und stellen sicher, dass jede Benutzerin und jeder Benutzer über ein positives Nettovermögen verfügt.
Der Gesamtwert, den die Börse beansprucht, gilt für jede einzelne Benutzerin und jeden einzelnen Benutzer. Die Benutzerinnen und Benutzer sollten daher in der Lage sein, die Einbeziehung des Nettowerts in den Gesamtwert zu überprüfen
Das Offenlegen dieser Guthaben kann jedoch die Privatsphäre der Benutzerinnen und Benutzer gefährden. Um dies zu lösen, verwenden wir eine Methode namens Zero Knowledge Proof (ZKP) , um die Privatsphäre der Benutzerinnen und Benutzer zu schützen.
Zero-Knowledge-Proof (ZKP)
Es ist eine Sicherheitstechnik, die es Kryptowährungsbörsen ermöglicht, zu beweisen, dass eine Aussage wahr ist, ohne zusätzliche Informationen preiszugeben.
In unserem Fall wollen wir nachweisen, dass wir genügend Geldmittel haben, ohne spezifische Benutzerdetails weiterzugeben. Die meisten ZKP fallen in zwei Kategorien:
zk-SNARK
zk-STARK
Wir verwenden zk-STARK, weil es sicherer ist und eine minimale Sicherheitsannahme hat. In diesem Artikel erklären wir, wie wir zk-STARK verwenden, um die Privatsphäre der Benutzerinnen und Benutzer zu schützen, während wir unsere Solvenz nachweisen. Bevor wir fortfahren, ist es hilfreich, einige grundlegende ZKP-Begriffe zu verstehen, wie Circuit, Merkle-Baum und Verpflichtungen.
Für Anfängerinnen und Anfänger gibt es viele Ressourcen, die Ihnen helfen, den Einstieg zu finden. Fortgeschrittene Benutzerinnen und Benutzer können sich den MOOC-Kurs und die wissenschaftliche Monografie anschauen.
Wie funktioniert zk-STARK?
Wir erstellen einen Merkle-Baum, indem wir den Hash jedes Benutzerkontos als Blätter verwenden. Jedes Konto zeigt Guthaben in USD für verschiedene Token (z.B. BTC, ETH) an. Um mit diesen Guthaben umzugehen, trennen wir die Guthaben in nicht-negatives Eigenkapital und Schulden für jeden Token. Auf diese Weise arbeiten wir nur mit positiven Zahlen, was es einfacher macht, Berechnungen zu verarbeiten und Fehler zu vermeiden.
Zum Beispiel:
Wenn das BTC-Token-Guthaben eines Benutzers A ist, ist sein BTC-Eigenkapital A und seine BTC-Schulden sind 0
Wenn das Guthaben der ETH-Token eines Benutzers -B beträgt, ist das entsprechende Eigenkapital 0 und die Schulden sind B
Anschließend bauen wir einen Merkle-Tree mit diesen Kontowerten als Blätter auf. Die Wurzel des Baums fungiert als ein einzelner Wert, der alle Benutzerguthaben repräsentiert. Jede Benutzerin und jeder Benutzer kann nachweisen, dass ihr oder sein Konto Teil dieses Baumes ist, indem sie oder er einen Merkle-Pfad verwendet, der zeigt, wie ihr oder sein Konto mit der Wurzel verbunden ist.
Wir veröffentlichen auch das gesamte Eigenkapital und die Schulden, die über alle Token und Benutzerinnen und Benutzer hinweg gezogen werden. Anschließend erstellen wir einen Zero-Knowledge-Proof (ZKP), um zwei Dinge zu zeigen:
Summenbeweis: Die Eigenkapital- und Schuldenwerte im Merkle-Baum addieren sich korrekt
Nicht-negativer Beweis: Das gesamte Eigenkapital jeder Benutzerin und jedes Benutzers ist größer als ihre oder seine Gesamtschuld
Wenn wir versuchen, den Merkle-Baum für eine große Anzahl von Konten zu überprüfen, wird es zu viel, um es auf einmal zu bewältigen. Um diese Herausforderung zu überwinden, teilen wir die Konten in kleinere Gruppen, die Batches genannt werden. Jeder Batch wird separat mit Batch-Circuits verarbeitet, die den unteren Teil des Merkle-Baums überprüfen.
Batchverarbeitung macht es nicht nur handhabbar, sondern ermöglicht es uns auch, diese Überprüfungen gleichzeitig (parallel) durchzuführen. Sobald wir die Ergebnisse aus jedem Batch haben, verwenden wir eine weitere Schicht von Circuits, die rekursive Circuits genannt werden, um alle Batches zusammenzuführen und zu überprüfen, bis wir den gesamten Merkle-Baum nachgewiesen haben.
Was ist Batch Circuit?
Der Batch-Circuit nimmt 1024 Konten (acc0, acc1,..., acc1023) als Eingaben und erzeugt 3 Hauptausgaben: einen Hash (hbatch), einen Gesamtwert des Eigenkapitals (ebatch) und einen Gesamtwert der Schulden (dbatch). Er prüft dabei folgende Punkte:
Das gesamte in USD denominiertes Eigenkapital jedes Kontos ist größer als seine Gesamtschulden
eBatch ist die Summe aller in USD denominierten Eigenkapitalwerte über diese Konten
dBatch ist die Summe aller in USD denominierten Schuldenwerte über diese Konten
hBatch ist die Wurzel des Merkle-Baums, der mit den Hashes der Konten erstellt wurde
Es gibt keine Überlauf während der Summierung für ebatch und dbatch
Was ist ein Rekursiver Circuit?
Der rekursive Circuit nimmt 64 verschiedene Beweise (π0, ..., π63), Hashes (h0, ..., h63), Eigenkapital (e0, ..., e63) und Schulden (d0, ..., d63) von den unteren Circuits als Eingaben. Es kombiniert diese Eingaben und erzeugt 3 Ausgaben: einen neuen Hash (hrekursiv), das Gesamteigenkapital (erekursiv) und die Gesamtschulden (drekursiv). Er prüft dabei folgende Punkte:
Jeder der 64 Nachweise ist gültig
Jeder Beweis π0, ..., π63 aus dem unteren Circuit ist gültig.
erekursiv ist die Summe von e0, ..., e63
drekursiv ist die Summe von d0, ..., d63
hrekursiv ist der Hash der Verkettung von h0, ..., h63, d.h.
hrekursiv = Hash (h0 || h1 || ... || h63)
Es gibt keine Überlauf während der Summierung für erekursiv und drekursiv
Was ist die Beziehung zwischen Batch-Circuit und rekursiven Circuits?
Das Diagramm unten zeigt, wie Batch-Circuit und rekursiver Circuit miteinander verbunden sind und Daten austauschen. Bitte beachten Sie, dass wir im Diagramm die Circuits zu Illustrationszwecken duplizieren, aber in unserer Implementierung verwenden wir nur einen Circuit für jede Ebene.
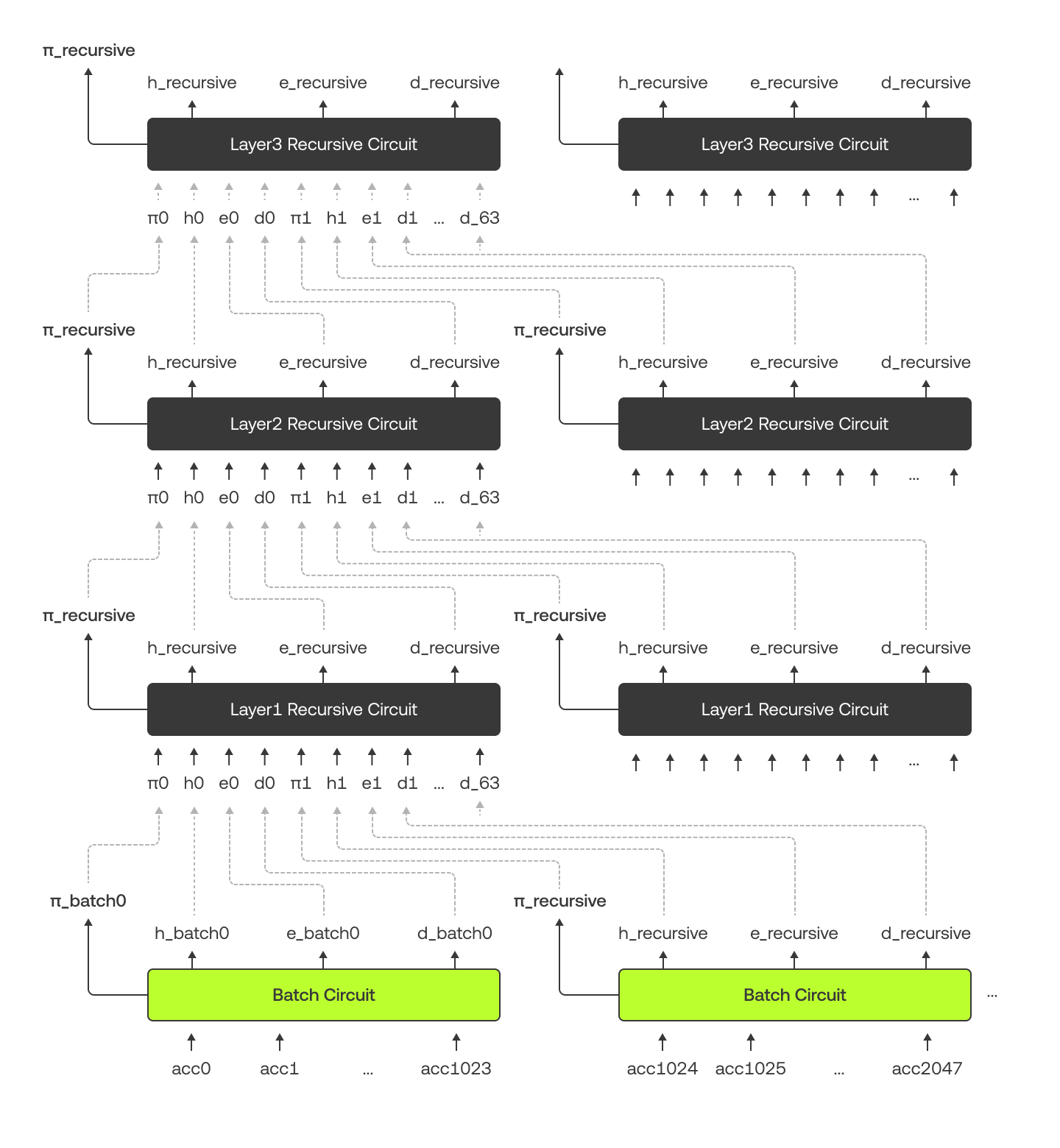
Unser Merkle-Baum ist etwas anders strukturiert. In den unteren 10 Ebenen hat jeder Elternknoten 2 Kinder, während in den oberen Ebenen jeder Elternknoten 64 Kinder hat. Das liegt daran, dass der Batch-Circuit den unteren Teil bearbeitet und die rekursiven Circuits den oberen Teil verwalten. Das Diagramm unten verwendet ein Beispiel mit „Alice“, um den Merkle-Baum und ihren Merkle-Beweis (grün eingefärbt) zu zeigen.
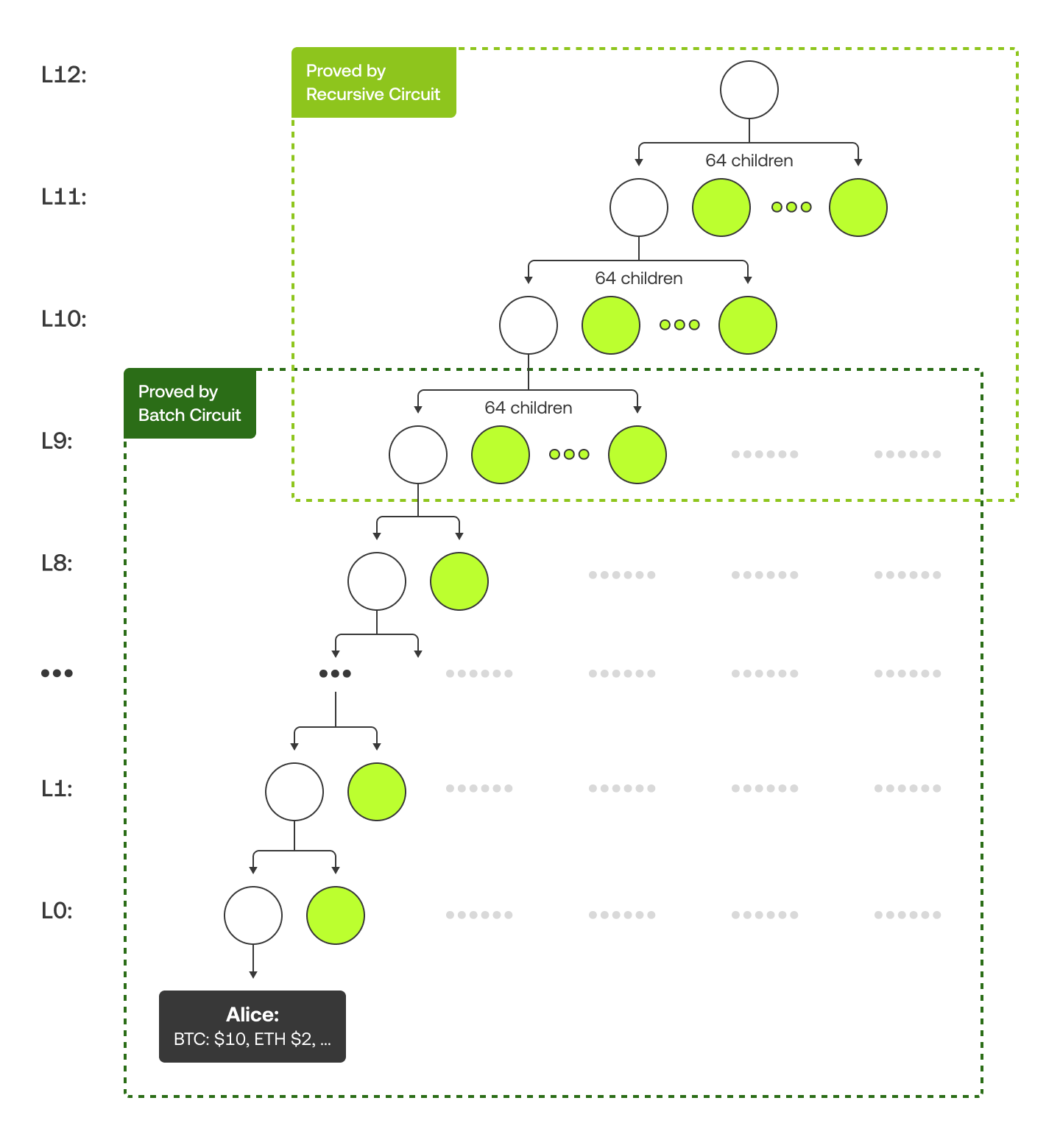
Für weitere technische Details, wie wir Kontonummern an die Batchgröße anpassen oder den richtigen Hash-Algorithmus auswählen, besuchen Sie diese Seite.
Fortschritte in zk-PoR Version 2
Unsere zk-PoR Version 2 hat mehrere Fortschritte gegenüber der vorherigen Version gemacht:
Größere Effizienz: Es ist jetzt 50 Mal schneller als die vorherige Version. Es dauert 3 Stunden auf einer einzelnen 10-Kern-Maschine, im Vergleich zu 36 Stunden der vorherigen Version mit neun 64-Kern-Maschinen. Dieser Geschwindigkeitszuwachs ist auf die Verwendung des Plonky2-Frameworks zurückzuführen, das in Rust codierte Circuits in effizienten Maschinencode kompiliert, anstatt langsamere Python-Skripte zu verwenden. Wir haben Plonky2 auch verbessert, um einige Berechnungen auf GPUs auszuführen, was die Zeit um zusätzlich 30 % reduziert.
Bessere Nachvollziehbarkeit: Mit Version 2 verwenden wir ein hochrangiges Framework, das komplexe kryptografische Details für uns verwaltet. Dadurch wird unser Code deutlicher, lesbarer und weniger anfällig für Fehler.
Kompakte Beweisführung: Die V2-Beweisgröße (~500KB) beträgt nur 0,05% von V1 (~1,2GB). Dank der rekursiven Methode können die Nachweise wiederholt aggregiert und zu einem einzigen Nachweis zusammengefasst werden.
Wie führe ich eine Selbstverifizierung des Proof of Reserves (PoR) durch?
So überprüfen Sie, ob das Guthaben Ihrer Vermögenswerte als zk-STARK Merkle-Blatt enthalten ist:
Melden Sie sich bei Ihrem OKX-Konto an, gehen Sie zu Vermögenswerte und wählen Sie PoR-Berichte aus
Wählen Sie Details aus, um Ihre Prüfungsdaten anzuzeigen
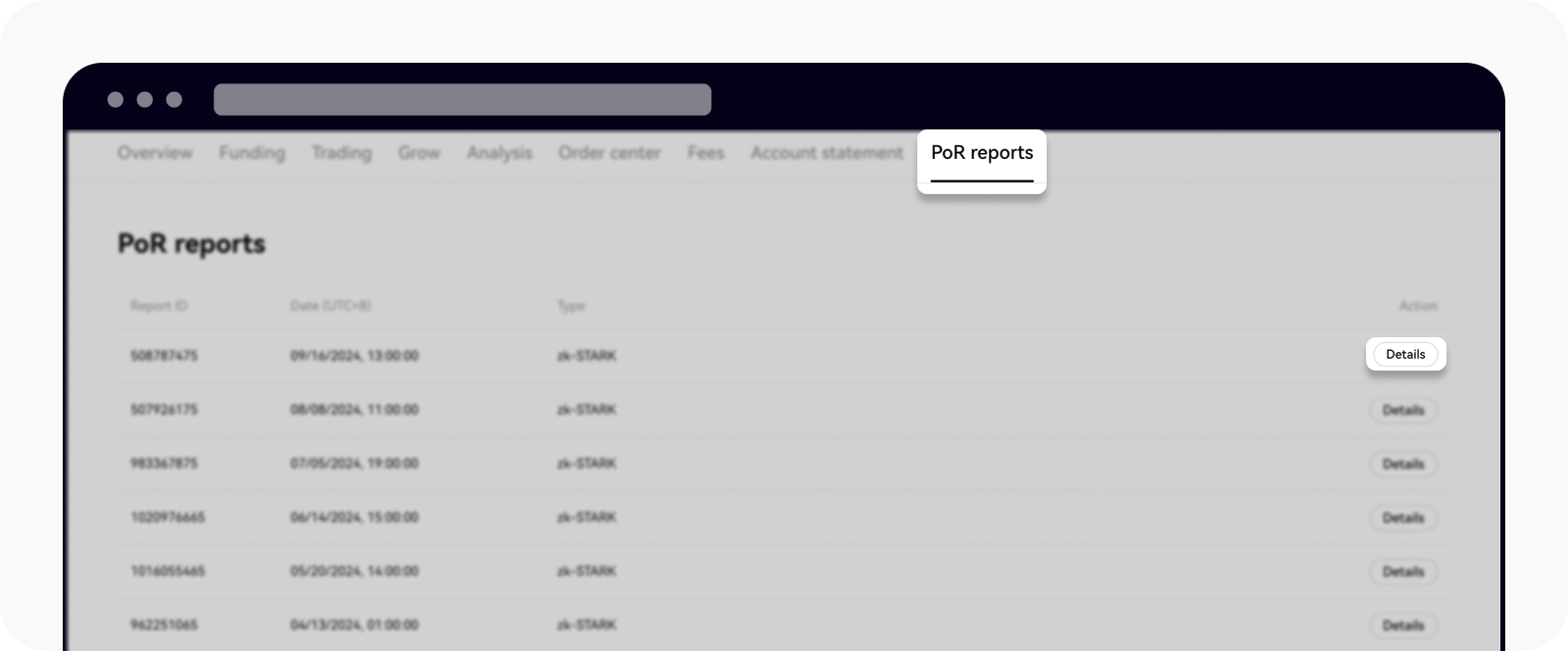
Die für die manuelle Verifizierung erforderlichen Daten erhalten Sie über die Schaltfläche Daten kopieren
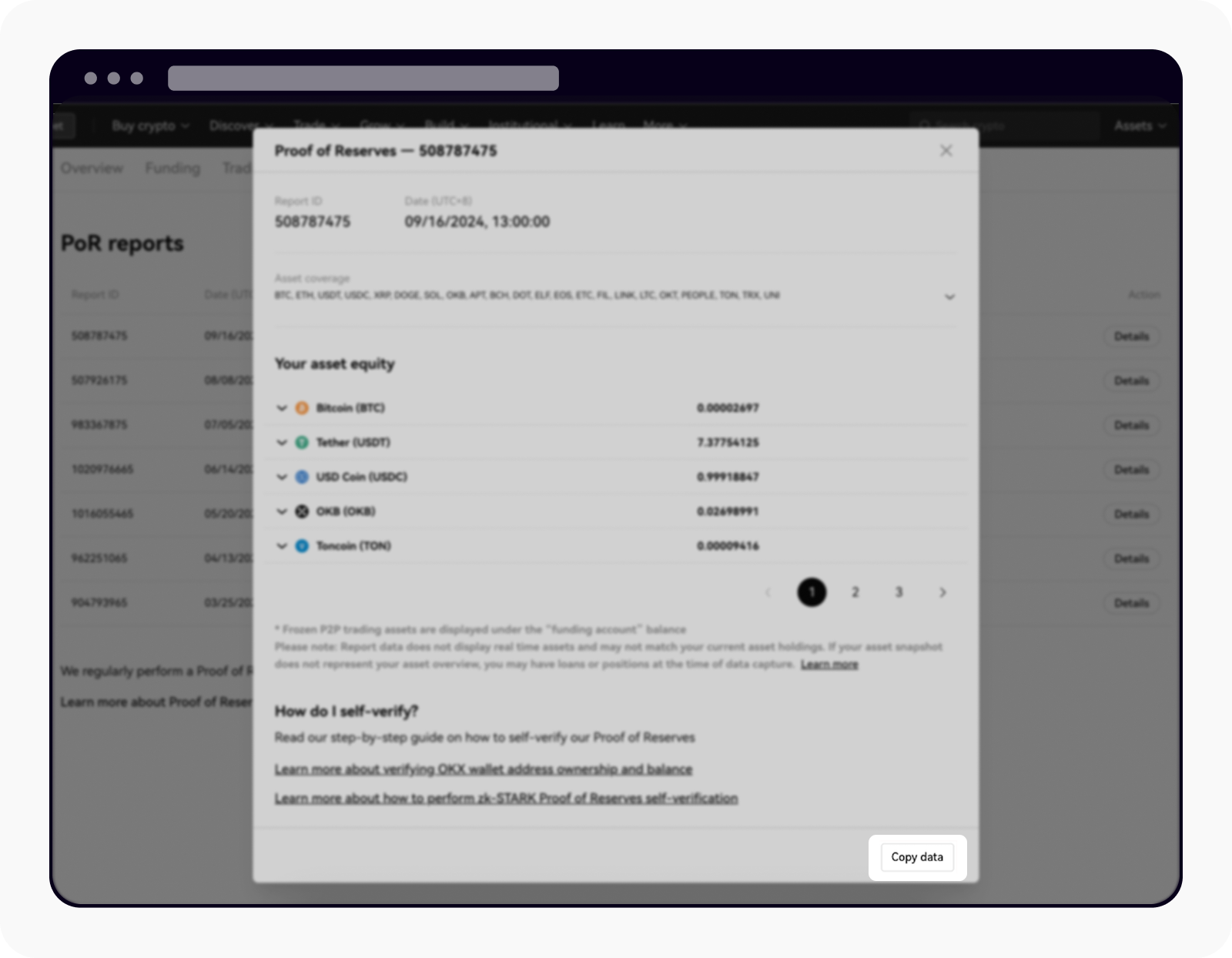
Nachdem Sie auf Daten kopieren geklickt haben, öffnen Sie den Texteditor (z. B. Notepad/Windows-Editor), fügen die Daten ein und speichern den JSON-String als JSON-Datei. Die Datei muss mit dem Zusatz „_inclusion_proof.json.“ enden. Die JSON-Zeichenfolge enthält Ihren Kontostand und eine Momentaufnahme des Merkle-Pfads und speichert die Datei dann in einem neuen Ordner
Öffnen Sie einen Texteditor (z. B. Notebook), fügen Sie die JSON-String ein und speichern Sie ihn als Datei. Der Dateiname muss mit „_inclusion_proof.json.“ enden. Speichern Sie die Datei in einem neuen Ordner.
Die JSON-String enthält Ihren Kontostand und eine Momentaufnahme des Merkle-Pfads.
Der JSON-Text wird unten angezeigt:
{"sum_tree_siblings":["9ffb169fecf075e203edca2af65e4c69fa4331d13ac75ccae4cd5b990c91b675","7149661a789763cb61293ebf5d8bdd5570e79ee203738f87a444c79642b89a79","788aac9e392fa62bc3f79c98c7afd7bb41ee7d5bd496876cd0580080f19e002f","e828a44d345e6799e232aabc57cb2b92986ee1c52b65344d83e79d84b4b571b7","6c0675de9cd6b2be1abd6a98260e7ea776492c4aa9aadf31086f23452cb7c48d","2dfe3aadb5ac00ee0b1110ee8c313afdee85d9f9c62904d6ee79c8f02354d80a","5068ae26192587432892a6de8b54ea25a8aafd1c010ab5e67b55b2c30c6257fa","a1bb026ec9f3d8a1fa1b6f498c40ed8b117a57e1af9816d08d9135ab4fe43a60","119dfcd214191405b7f7f7c7091b89196c0cae818bfcd8252a48f20d9cf3c378","4d9403482ca177c669df34a60bb2afab7a18097012d0b70703c8e59258cdfee6"],"recursive_tree_siblings":[{"right_hashes":["e041eaa366259f873e9e1477aac77362f4b1b460c2d5e1c14907fa9288d66cff","b45a8c503e649ff39543a918996b06fc65f4df9b61d071b22f7342f94862c9be","e00ec1225dfe6b7e950f6b9b8e9d1121bf17eb60c444fd7191b861a2ddddad23","c02c12beb73c03f996508cdce7bef927f0aa8b77ebd899f6a75df83de9d4022e","d36b95f14c5fd5bfaf1347e3177340e2fc9475a77b852321b80527132e7d539c","c0b9770178e70a7bba4ac8aeaadab2bcb2ae7f90d0f678bd463f2c42ff4f4a7b","fab5e7c6f7f8bc6d51f515c5db235cc1ebe987adee8c19c9bc7313e9e266d72c","b3884fb88fc95949c78ca8867cfa9e8a3c4c59fa1a48d8371f7fbfbebda0acfd","0c6da9bdbd40065f92ddaa45297670f2f0bffedb74020c5d5752e70d8b507b77","left_hashes":["1101beee3c6a36a168ceee9d43fcf6cb6de7e5c87ed4d22cd0308c9870d17839","d40a8e9eb4c873996ec515600def480eaa9378ca8481a7bcdf5f77725dbec4ae","63b12566ba8473f502386e92d500664cb63683dca6c26593378dcc9715257b77","166440a8ccbfbc1ce6ec5efaf8bc0b25e1bf692fa972e2729e45ce709d1d35a3","724451ad1d937fc47de5ede930d159dce78093d5e6a1f2e698452f8a29b4de3a","081a88f12d4e23173a1bf5038d4a9413cc92dd421c92261065de06492b5010ec","a76dbb1d4c393539b9546f4460d50ebc7582748d7de63c62c463b793c55bac7c","91e6c21de3f4060e1bd864131a570af42de31bbcd84a5afcbbc8fedcbf806002","fad08eca5bfdc5f37d39eabb44c2216afc6498afcb6b913d72586eaaf132a572","d39b06fe28387ba8045e2b2f95e90613916beef4f79df7961514e6e4cbfd07fa","81d07e300a116a0e4fcb56c39715c5fd5921abe8d10329b07c3f33d417b70ca8","7b72a7e62a45c9958a8a55eec2ba47352f2af701bacba098668589f6a3ce0423","8766bc64c38c2bb4188d89de0e732bca103daaed0c779cba9a8b191e24b51c9c","fa57ae4409e46c605f3cbfd01dfd9ccebc86cbd765cdc067206cb9367832442f"]}, ...... "index":9583119,"account":{"id":"50f5f08cc5036e15a541c64ac4ac6d2d9aa8ddab1ec32ed58b10e6ed3edfad59","debt":["0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0"],"equity":["8412384","9386185","45265193","0","0","8751","3824171","2716990","0","313671","28319","0","0","0","41261","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","142353","0","0","0","0","0","4435","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","662","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","993","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","25132","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","305","0","0","0","0","0","0","0","0","6141","0","0","0","0","0","0","0","0","0","0","0","5511","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0"]}}
Laden Sie das OKX Open-Source-Verifizierungstool zk-STARKValidator herunter
Speichern Sie das OKX Open-Source-Verifizierungstool zk-STARKValidator und die JSON-String-Datei zusammen im neuen Ordner, den Sie in Schritt 5 erstellt haben. In unserem Fall speichern wir das Tool und die Datendatei im Ordner Downloads unter der Bezeichnung „proof-of-reserves“, wie unten dargestellt:

Öffnen Sie den zk-STARKValidator. Er führt die JSON-Datei, die Sie im Ordner gespeichert haben, automatisch aus
Überprüfen Sie das Ergebnis:
Wenn die Verifizierung erfolgreich ist, wird das Ergebnis Validierung der Einschlussbeschränkung bestanden angezeigt:

Wenn die Verifizierung fehlschlägt, wird das Ergebnis Validierung der Einschlussbeschränkung fehlgeschlagen angezeigt:

Wie verifiziere ich das Gesamtguthaben und die nicht-negativen Einschränkungen von zk-STARK?
So verifizieren Sie, ob die von uns gehaltenen Vermögenswerte korrekt sind und dass keine Benutzerin und kein Benutzer negatives Nettokapital besitzt:
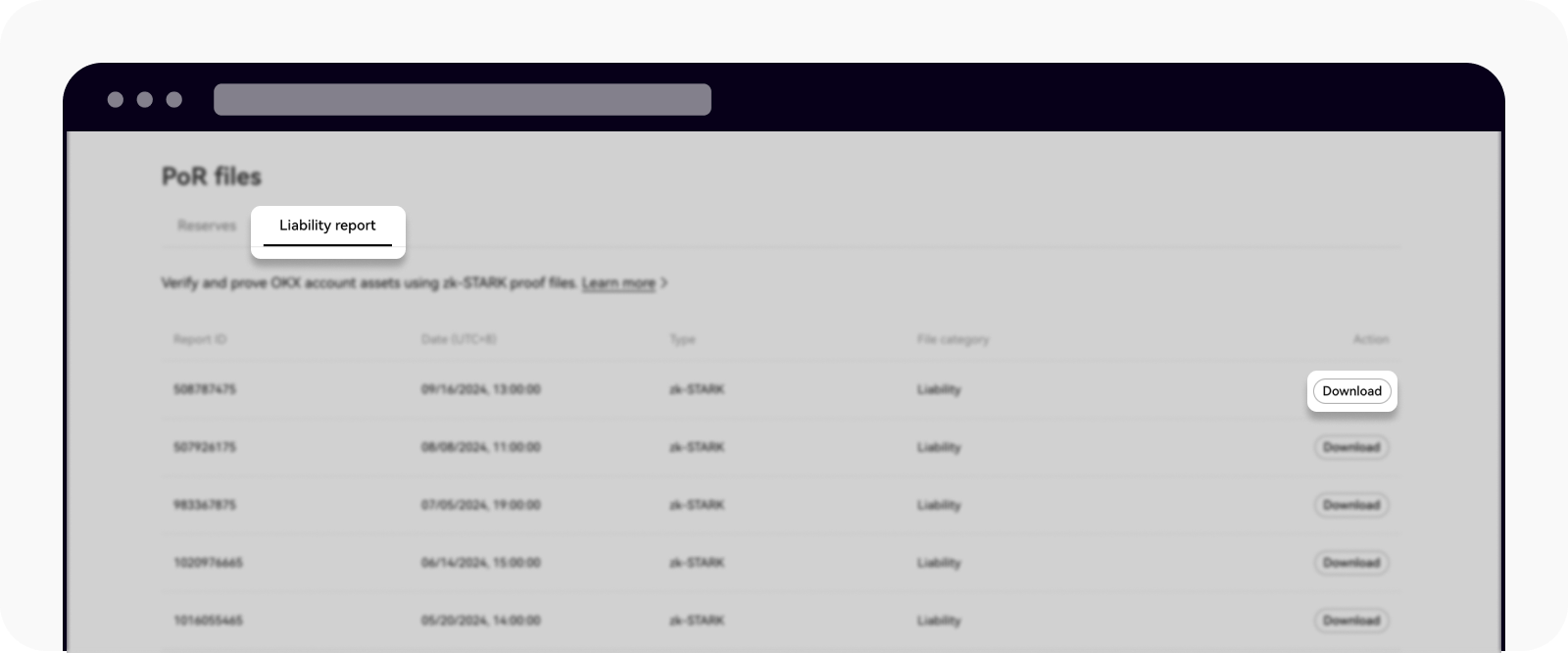
Gehen Sie zu unserer Seite Proof of Reserve und wählen Sie Haftungsbericht
Laden Sie die zk-STARK Datei herunter und speichern Sie sie in einem neuen Ordner
Entzippe die Datei, um eine "sum_proof_data.json"-Datei zu extrahieren

Laden Sie das OKX Open-Source-Verifizierungstool zk-STARKValidator herunter
Speichern Sie das Open-Source-Verifizierungstool von OKX, zk-STARKValidator, und die „sum_proof_data.json“ Datei zusammen im neuen Ordner, der in Schritt 2 erstellt wurde. In unserem Fall speichern wir das Tool und die Datendatei im Ordner Downloads unter der Bezeichnung „proof-of-reserves“, wie unten dargestellt:

Öffnen Sie den zk-STARKValidator. Er führt die Summennachweisdaten, die Sie im Ordner gespeichert haben, automatisch aus
Überprüfen Sie das Ergebnis
Wenn die Verifizierung erfolgreich ist, wird das Ergebnis Gesamtsumme und nicht-negative Einschränkungsvalidierung bestanden angezeigt:

Wenn die Verifizierung fehlschlägt, wird das Ergebnis Gesamtsumme und nicht-negative Einschränkungsvalidierung fehlgeschlagen angezeigt:

Um weitere technische Details zu erkunden, ist unser Proof of Reserves-System Open Source und zur Überprüfung und Nutzung auf github verfügbar.






